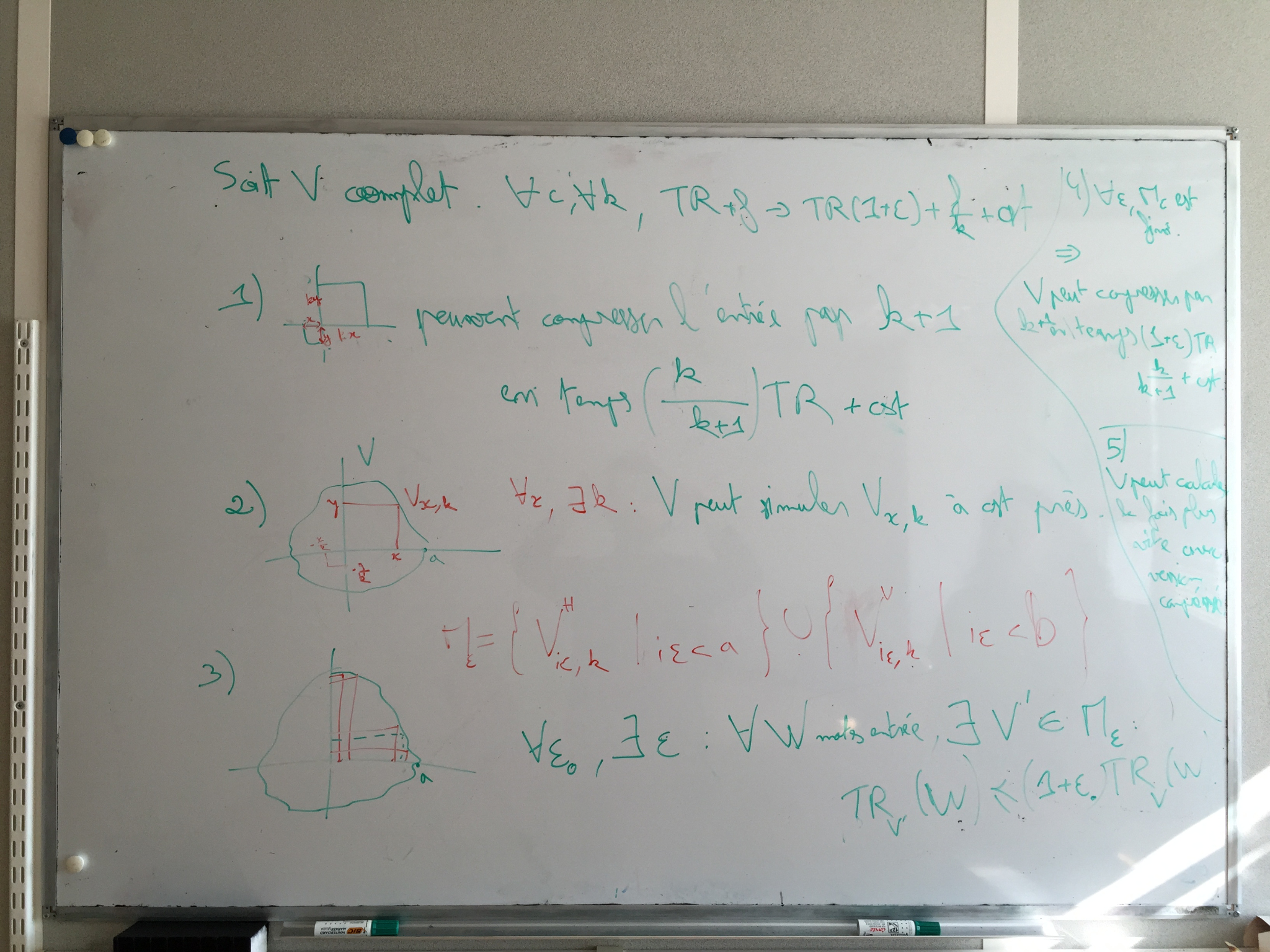Cellular Automata
2-dimensional cellular automata (2DCA) \(\ACA = (\ACQ, V, \delta)\) :
- \(\ACQ\) is a finite set (states)
- \(V\) is a finite subset of \(\ZZ^2\), \(0\in V\) (neighborhood)
- \(\delta:\ACQ^{V}\rightarrow \ACQ\) (local function)
global function \(\Delta: \ACQ^{\ZZ^2}\rightarrow \ACQ^{\ZZ^2}\)