\( \newcommand{\llbracket}{[\![} \newcommand{\rrbracket}{]\!]} \renewcommand{\epsilon}{\varepsilon} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\NN}{\mathbb{N}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\ACA}{\mathcal{A}} \newcommand{\ACC}{\mathcal{C}} \newcommand{\ACV}{\mathcal{V}} \newcommand{\ACQ}{\mathcal{Q}} \)

Accélération constante

Proposition

Tout langage reconnu en temps \(\TR + k\) (\(k\geq 0\)) par un AC fonctionnant sur le voisinage de Moore est reconnu en temps réel par un AC sur le même voisinage.

Proposition

Tout langage reconnu en temps \(\TR + k\) (\(k\geq 0\)) par un AC fonctionnant sur le voisinage de von Neumann est reconnu en temps réel par un AC sur le même voisinage.

Les preuves sont différentes
Le résultat se généralise à des classes de voisinages plus larges
On ne sait pas si le résultat est vrai pour tout voisinage

Voisinage de Moore

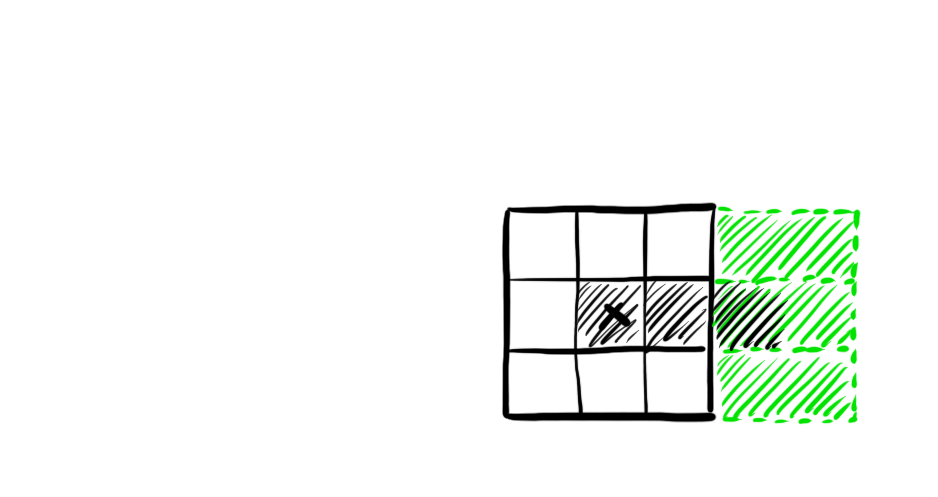
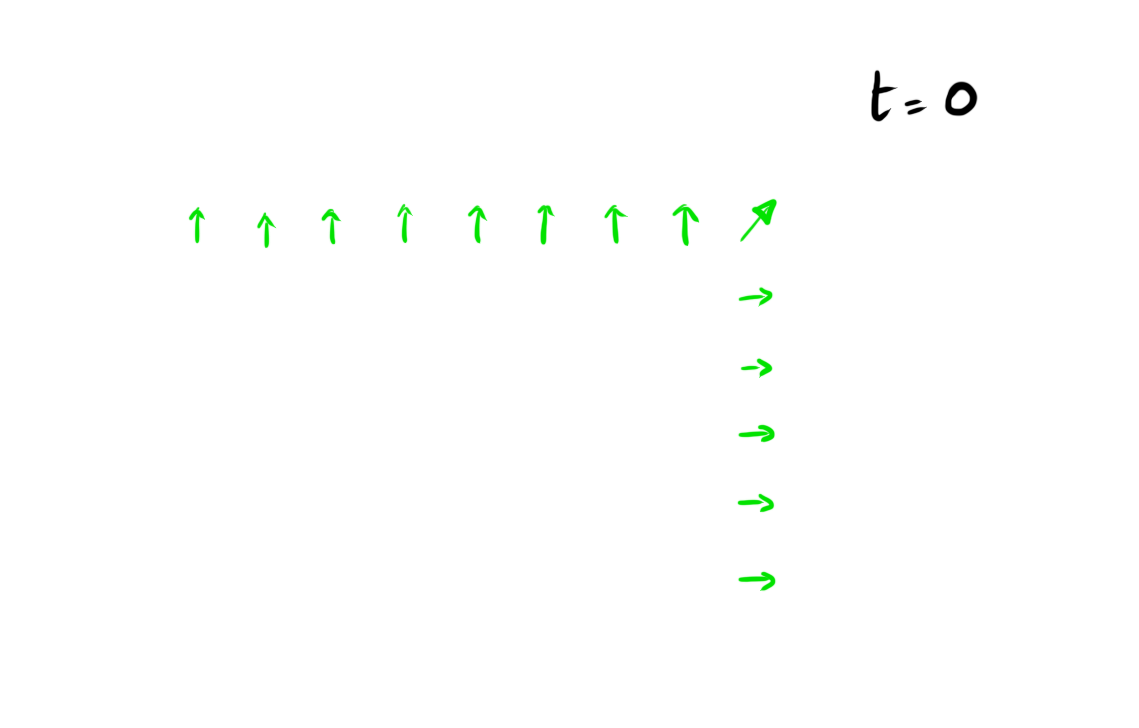
Sur le voisinage de Moore, l'accélération constante est similaire au cas 1D

les cellules essaient de deviner les états en haut et à droite
les cellules au bord sont correctes
la correction se propage vers l'origine
l'origine est correcte au temps réel et peut anticiper \(k\) étapes de calcul

Voisinage de von Neumann

La même méthode ne fonctionne pas directement (il manque des informations pour propager la correction)

On commence par emmagasiner des informations (1 étape)
Les cellules devinent l'état en haut à droite
La correction se propage correctement si les voisines en haut et à droite sont correctes
Les cellules en bas (resp. à gauche) devinent aussi l'état de leur voisine en haut (resp. à droite)

Voisinage de Moore

Théorème

Pour tout \(\epsilon > 0\), tout langage reconnu en temps \((\TR+f)\) par un AC sur le voisinage de Moore peut être reconnu en temps \((\TR + \lceil \epsilon f\rceil)\) sur ce même voisinage

Idée de la preuve:

Compression de l'entrée d'un facteur \(k \geq \epsilon^{-1}\)\(\frac{k-1}{k}\TR\) étapes
Simulation de l'automate initial \(k\) étapes à la fois\(\frac{1}{k}(\TR + f)\) étapes

Compression

Les cellules stockent \(k^2\) états de l'automate initial

les données vont vers l'origine
quand une cellule a \(k\times k\) états de l'AC initial, elle est pleine

Simulation

Preuve par récurrence

Chaque cellule doit voir \(V^k+c\) pour chaque \(c\) qu'elle contient
Les données sont présentes sur ses voisines
Chaque cellule peut calculer \(k\) étapes de l'automate initial pour tous les états qu'elle contient

Synchronisation

Problème : Les cellules ne finissent pas la compression en même temps

Solution : Simuler l'automate initial dès que les données sont disponibles

\(V\) complet
différence de temps entre voisines borné par \(k\) tel que \(-V\subseteq V^k\)
cellules connaissent leur temps simulé modulo \((2k+1)\) et leurs \(k\) états précédents
la dernière cellule n'a jamais à attendre

Voisinage quelconque

Théorème

Pour tout voisinage complet \(V\) et tout \(\epsilon>0\), tout langage reconnu en temps \((\TR + f)\) par un AC sur \(V\) peut être reconnu en temps \((1+\epsilon)\TR + \epsilon f\) sur le même voisinage

Idée de la preuve:

Compression de l'entrée d'un facteur \(k \geq \epsilon^{-1}\)
Simulation de l'automate initial \(k\) étapes à la fois

Simulation

Problème : Après compression, une cellule voit \(kV+c\) pour les états qu'elle contient, pas \(V^k+c\)

Solution : Stocker plus d'information !

\(m = (k-1)|V| - k + 1\)
\(V^{m+k} \subseteq V^m + kV\)
chaque cellule stocke \(V^m +c\) pour les états qu'elle contient

À chaque étape, les cellules calculent \(k\) étapes de l'AC initial pour tous les états qu'elles contiennent

Enveloppe convexe

Def.

L'enveloppe convexe de \(V\) est le plus petit polygone convexe contenant \(V\)

Les sommets de l'enveloppe convexe sont des éléments de \(V\)

Prop.

Si \(V\) est complet, son enveloppe convexe contient une boule ouverte autour de l'origine

Prop.

\(\forall x\in\QQ^2\), si \(x\) est sur le bord de l'enveloppe convexe alors

\(x = \lambda u + (1-\lambda) v\)

avec \(u, v\in V\) et \(\lambda \in [0, 1]\cap \QQ\)

Compression

Problème : Le chemin optimal vers l'origine dépend du rapport \(\frac{m}{n}\)

Le chemin optimal est une combinaison de 2 sommets de l'enveloppe convexe de \(V\)
Exemple : sur le voisinage de Moore, mouvement diagonal et horizontal/vertical

Idée :

Si le voisinage est de type Moore, on peut compresser optimalement
Approximation des autres voisinages par des voisinages de type Moore
On peut compresser « presque » optimalement

Voisinages de type Moore

Définition : cf. illustration

Prop.

Sur un voisinage de type Moore, on peut compresser l'entrée par un facteur \((k+1)\) en temps

\(\frac{k}{k+1}\TR\)

Preuve : Comme pour le cas du voisinage de Moore

Proportion fixée

Pour des mots d'entrée de proportion fixée \(\rho\), le voisinage complet \(V\) peut se comporter comme un voisinage de type Moore \(V'\)

\(V\) est complet donc il contient une copie réduite du rectangle dans le quart de plan négatif
\(V\) et \(V'\) ont le même temps réel pour les mots de proportion \(\rho\)

Proportion approchée

On fixe \(\epsilon > 0\)
Soit \(M_\epsilon\) un ensemble des voisinages de type Moore couvrant \(V\) espacés d'au plus \(\epsilon\)

Pour tout mot en entrée, il y a un \(V'\in M_\epsilon\) qui peut le compresser d'un facteur \((k+1)\) en temps

\((1+\epsilon)\frac{k}{k+1}\TR_V\)

Bilan

Choisir \(\epsilon\) petit et \(k > \epsilon^{-1}\)
Compresser l'entrée d'un facteur \(k+1\) sur tous les voisinages de type Moore de \(M_\epsilon\)\((1+\epsilon)\frac{k}{k+1}\TR\)
Stocker un voisinage plus grand sur chaque cellule après compression\(O(1)\)
Simuler l'automate initial \((k+1)\) étapes à la fois\(\frac{TR+f}{k+1}\)

Temps total : \((1+\epsilon)\TR + \epsilon f\)

Accélérations en 2D

Accélération constante

Accélération constante

Voisinage de Moore

Voisinage de von Neumann

Accélération linéaire

Voisinage de Moore

Compression

Simulation

Synchronisation

Voisinage quelconque

Simulation

Enveloppe convexe

Compression

Voisinages de type Moore

Proportion fixée

Proportion approchée

Bilan